Toán Học Thuật

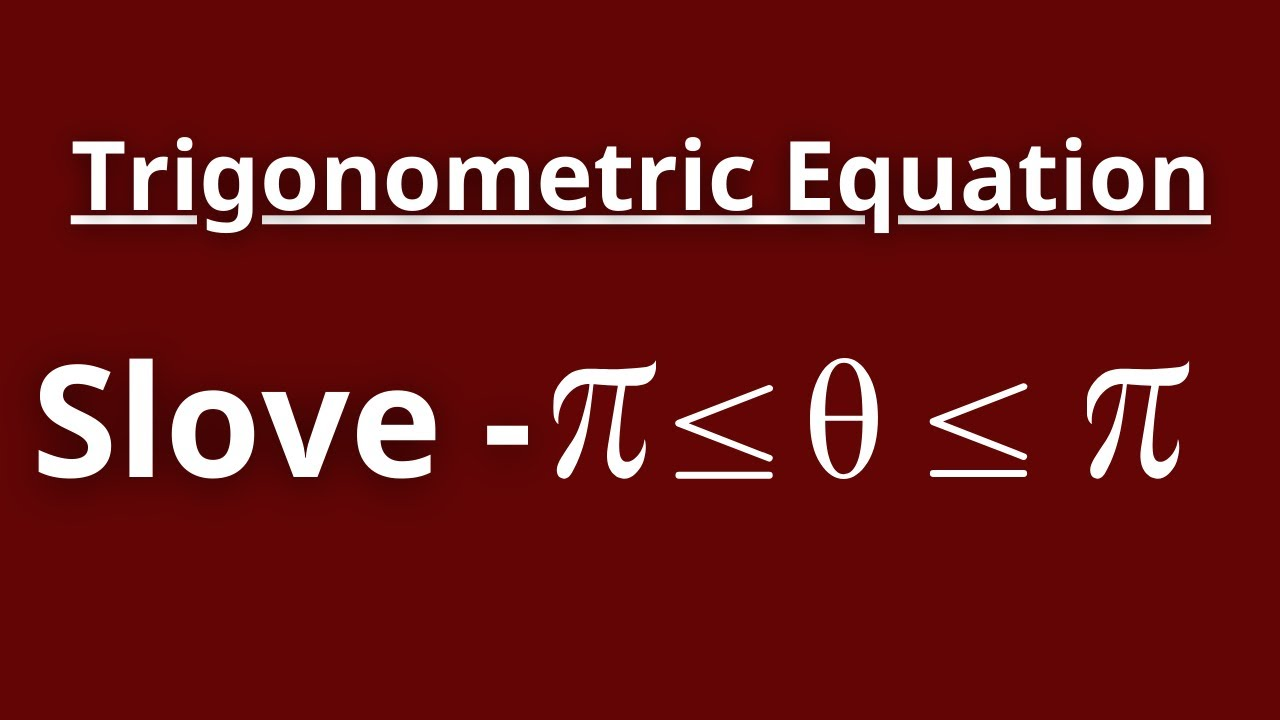
Solving advanced trigonometric equations requires not just knowledge of trigonometric identities, but also strategic application of algebraic techniques and a systematic approach to finding all solutions. At HappyMath, we believe that mastering these techniques enables students to tackle even the most challenging problems with confidence.

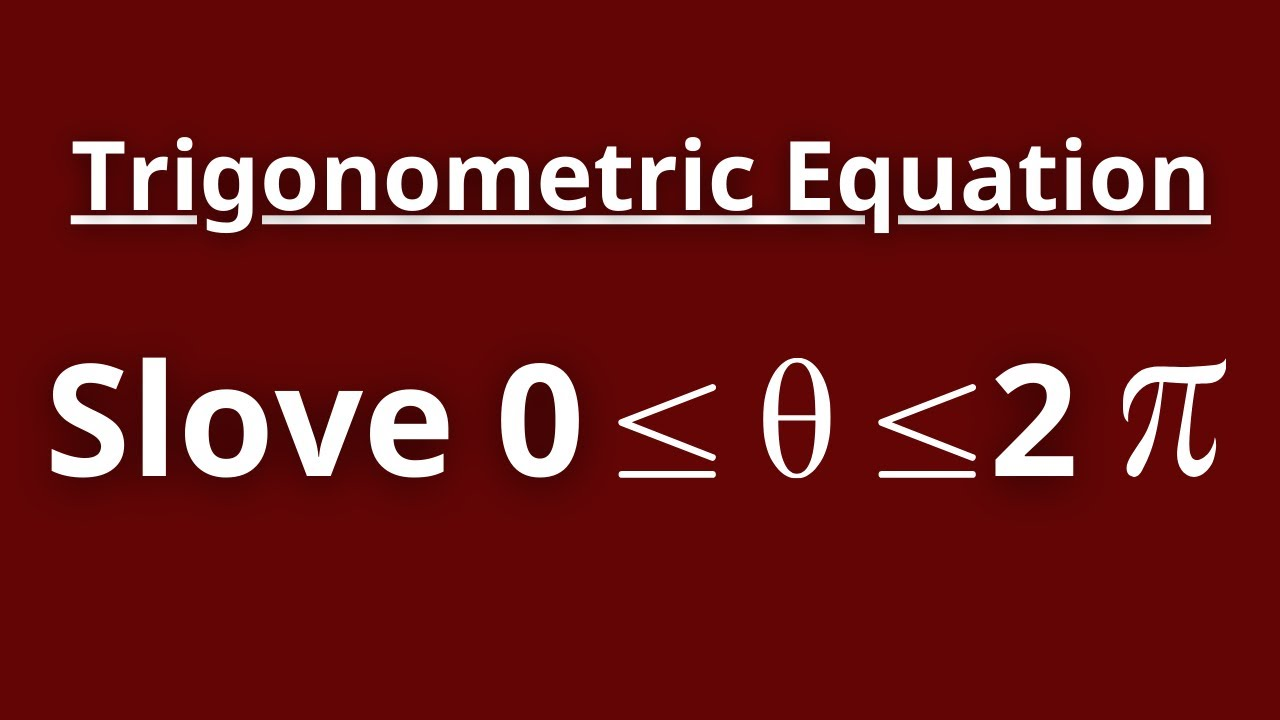
At HappyMath, we recognize that advanced trigonometric equations often require more than just standard trigonometric identities. Many complex problems demand a combination of algebraic techniques like factorization alongside trigonometric knowledge. This guide explores how to tackle equations where different trigonometric functions interact, requiring sophisticated solution strategies.

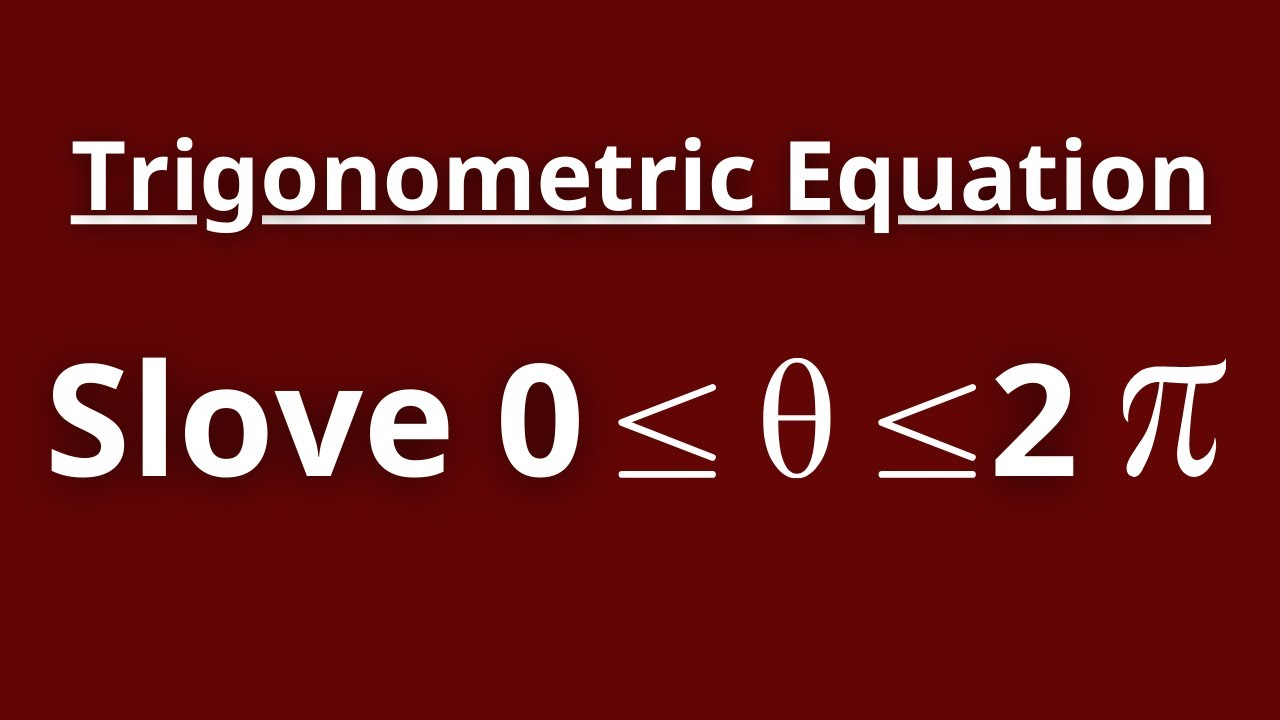
Trigonometric equations often require sophisticated techniques beyond basic algebraic manipulation. At HappyMath, we believe that mastering these advanced equations builds both technical skill and mathematical intuition. In this guide, we'll explore systematic approaches to solving complex trigonometric equations, including those involving multiple angles, double-angle formulas, and factorization techniques.

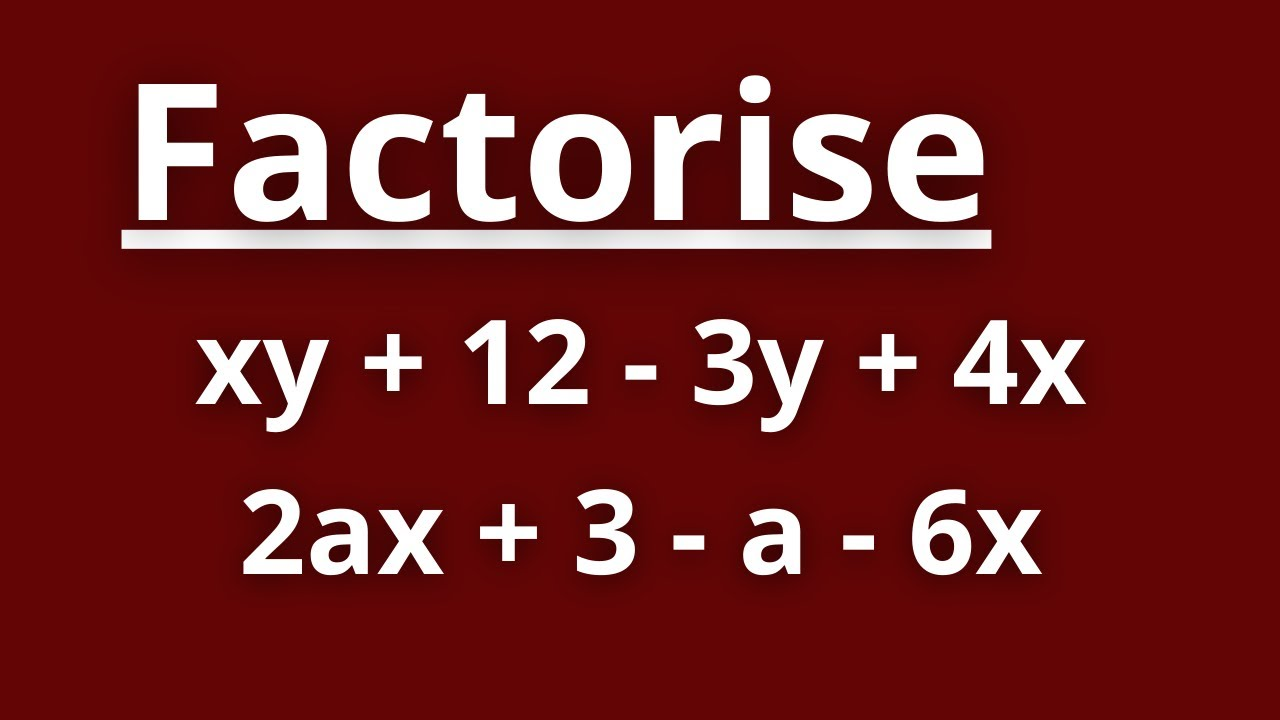
Advanced factorization often requires combining multiple techniques to solve complex expressions. At HappyMath, we understand that developing this skill requires both practice and a systematic approach.

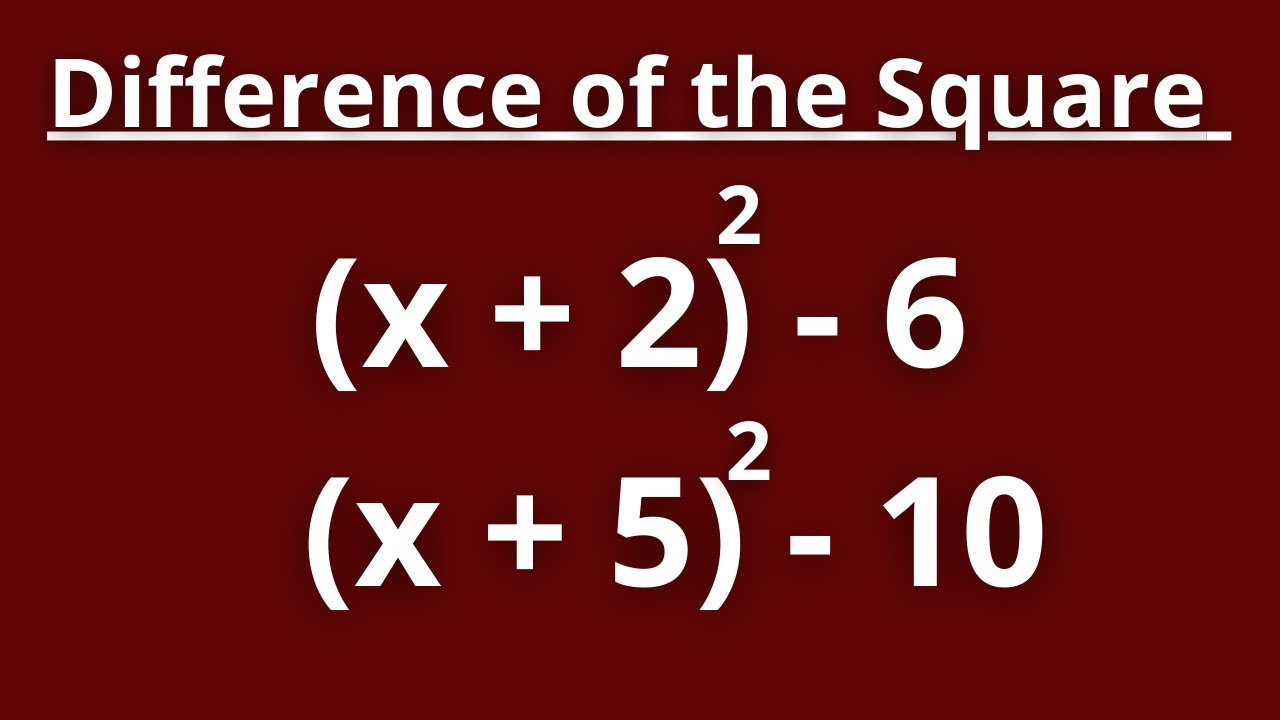
The difference of squares is a powerful factorization pattern that works with any expression of the form a² - b². When dealing with surds (expressions containing square roots), this pattern becomes particularly useful. At HappyMath, we recognize that mastering this technique opens doors to solving complex algebraic problems with elegance and precision.

Factorization is a fundamental skill in algebra that allows us to break down complex expressions into simpler components. At HappyMath, we believe that mastering factorization techniques is essential for success in algebra and higher mathematics. Whether you're solving equations, simplifying expressions, or analyzing functions, factorization serves as a powerful tool in your mathematical toolkit.

The difference of squares is one of the most versatile and powerful factorization techniques in algebra. At HappyMath, we consider it an essential tool in every student's mathematical toolkit. This pattern allows us to elegantly factor expressions of the form a² - b² into the product (a - b)(a + b).

Word problems involving exponential and logarithmic functions often require finding the values of unknown parameters. At HappyMath, we believe that mastering these techniques is essential for success in advanced mathematics. With the right approach, even complex problems become manageable.