Phép chia có dư - Division with Remainders

Phép chia có dư là một trong những khái niệm toán học cơ bản nhưng vô cùng quan trọng mà học sinh cần nắm vững ngay từ những năm đầu tiên làm quen với môn toán. Không chỉ đơn thuần là một phép tính số học, phép chia có dư còn là nền tảng để các em hiểu sâu hơn về mối quan hệ giữa các con số và vận dụng vào giải quyết các bài toán thực tế trong cuộc sống hàng ngày. Trong bài viết này, Happymath sẽ cùng bạn khám phá chi tiết về phép chia có dư, từ định nghĩa cơ bản đến các phương pháp tính toán và ứng dụng thực tế.

Phép chia có dư là gì?

Trước khi đi sâu vào các kỹ thuật tính toán và bài tập thực hành, chúng ta cần hiểu rõ bản chất của phép chia có dư. Đây là bước đầu tiên quan trọng giúp học sinh xây dựng nền tảng vững chắc cho việc học toán tiếng Anh sau này.

Phép chia có dư là một trong những khái niệm toán học cơ bản

Định nghĩa phép chia có dư

Phép chia có dư (division with remainders) là phép toán trong đó một số nguyên được chia cho một số nguyên khác mà kết quả không phải là số nguyên hoàn hảo. Khi thực hiện phép chia, nếu số bị chia không chia hết cho số chia, phần còn lại được gọi là số dư (remainder). Về mặt toán học, phép chia có dư được biểu diễn dưới dạng: dividend ÷ divisor = quotient remainder r, trong đó dividend là số bị chia, divisor là số chia, quotient là thương số và r là số dư.

Các thành phần của phép chia có dư

Để hiểu rõ hơn về phép chia có dư, chúng ta cần nắm vững các thành phần cơ bản. Số bị chia (dividend) là số được chia, số chia (divisor) là số dùng để chia, thương số (quotient) là kết quả của phép chia và số dư (remainder) là phần còn lại sau khi thực hiện phép chia. Một điều quan trọng cần nhớ là số dư luôn nhỏ hơn số chia và không âm. Ví dụ, trong phép tính 17 ÷ 5 = 3 remainder 2, số 17 là dividend, 5 là divisor, 3 là quotient và 2 là remainder.

Công thức tổng quát

Công thức toán học biểu diễn mối quan hệ giữa các thành phần trong phép chia có dư là: dividend = (divisor × quotient) + remainder. Công thức này không chỉ giúp chúng ta kiểm tra kết quả phép chia mà còn là cơ sở để giải quyết nhiều dạng bài toán phức tạp hơn. Học sinh cần ghi nhớ và vận dụng thành thạo công thức này trong quá trình học tập và làm bài tập.

Cách thực hiện phép chia có dư

Sau khi đã nắm vững lý thuyết cơ bản, việc tiếp theo là học cách thực hiện phép chia có dư một cách chính xác và hiệu quả. Có nhiều phương pháp khác nhau để thực hiện phép chia có dư, mỗi phương pháp phù hợp với từng trường hợp cụ thể.

Phương pháp chia thủ công

Phương pháp chia thủ công (long division) là cách truyền thống và phổ biến nhất để thực hiện phép chia có dư. Đầu tiên, ta xác định số chia có thể "chứa" bao nhiêu lần trong số bị chia. Sau đó, nhân số chia với thương số vừa tìm được và trừ kết quả khỏi số bị chia để tìm số dư. Ví dụ, để tính 47 ÷ 6, ta thấy 6 × 7 = 42 (nhỏ hơn 47) và 6 × 8 = 48 (lớn hơn 47), vậy thương số là 7. Số dư được tính bằng 47 - 42 = 5, do đó 47 ÷ 6 = 7 remainder 5.

VViệc tiếp theo là học cách thực hiện phép chia có dư một cách chính xác và hiệu quả

Phương pháp chia ngắn

Đối với các phép chia đơn giản hơn, phương pháp chia ngắn (short division) có thể được sử dụng để tiết kiệm thời gian. Phương pháp này đặc biệt hiệu quả khi số chia là số có một chữ số. Học sinh chỉ cần chia từng chữ số của số bị chia cho số chia, viết thương số lên trên và chuyển số dư sang chữ số tiếp theo. Kỹ năng này đòi hỏi sự thành thạo trong bảng nhân và khả năng tính toán nhanh.

Sử dụng bảng nhân để hỗ trợ

Việc thuộc lòng bảng nhân (multiplication table) là chìa khóa để thực hiện phép chia có dư nhanh chóng và chính xác. Khi biết rõ bảng nhân, học sinh có thể dễ dàng xác định thương số mà không cần thử nhiều lần. Ví dụ, nếu cần chia 56 cho 7, việc biết 7 × 8 = 56 giúp ta ngay lập tức xác định được thương số là 8 và số dư là 0. Đây là lý do tại sao giáo viên luôn khuyến khích học sinh học thuộc bảng nhân từ sớm.

Các tính chất của số dư

Hiểu rõ các tính chất đặc biệt của số dư sẽ giúp học sinh giải quyết các bài toán phức tạp một cách dễ dàng hơn. Những tính chất này không chỉ có giá trị về mặt lý thuyết mà còn có nhiều ứng dụng thực tế.

Giới hạn của số dư

Một trong những tính chất quan trọng nhất của số dư là nó luôn nằm trong khoảng từ 0 đến (divisor - 1). Nói cách khác, số dư luôn nhỏ hơn số chia. Nếu số dư bằng hoặc lớn hơn số chia, điều đó có nghĩa là phép chia chưa được thực hiện hoàn chỉnh và thương số cần được điều chỉnh. Ví dụ, khi chia cho 8, số dư chỉ có thể là 0, 1, 2, 3, 4, 5, 6 hoặc 7.

Số dư bằng 0

Khi số dư bằng 0 (remainder equals zero), điều đó có nghĩa là phép chia được thực hiện hoàn toàn, hay còn gọi là chia hết (divisible). Trong trường hợp này, số bị chia là bội số của số chia. Việc xác định xem một số có chia hết cho số khác hay không là một kỹ năng quan trọng trong nhiều lĩnh vực toán học, từ phân tích số nguyên tố đến giải phương trình.

Hiểu rõ các tính chất đặc biệt của số dư sẽ giúp học sinh giải quyết các bài toán phức tạp

Quy luật về số dư

Số dư có nhiều quy luật thú vị mà học sinh có thể khám phá. Ví dụ, khi chia một số cho 2, số dư chỉ có thể là 0 (số chẵn) hoặc 1 (số lẻ). Khi chia cho 5, số dư có thể là 0, 1, 2, 3 hoặc 4, tương ứng với chữ số tận cùng của số bị chia. Những quy luật này giúp học sinh dự đoán và kiểm tra kết quả nhanh chóng mà không cần thực hiện phép chia đầy đủ.

Ứng dụng của phép chia có dư trong thực tế

Phép chia có dư không chỉ là một khái niệm toán học trừu tượng mà còn có vô số ứng dụng trong cuộc sống hàng ngày. Việc nhận ra những ứng dụng này giúp học sinh thấy được tầm quan trọng và ý nghĩa của những gì các em đang học.

Chia đều vật dụng

Một trong những ứng dụng phổ biến nhất của phép chia có dư là chia đều các vật dụng. Ví dụ, nếu có 23 cái kẹo cần chia đều cho 5 em nhỏ, mỗi em sẽ nhận được 4 cái kẹo (thương số) và còn thừa 3 cái (số dư). Điều này giúp chúng ta biết được số lượng mỗi người nhận được và số lượng còn lại cần xử lý như thế nào.

Xác định ngày trong tuần

Phép chia có dư còn được sử dụng để tính toán ngày trong tuần. Vì một tuần có 7 ngày, ta có thể sử dụng phép chia cho 7 để xác định ngày cụ thể. Các lập trình viên thường sử dụng phép toán modulo (dựa trên phép chia có dư) để giải quyết các vấn đề liên quan đến lịch và thời gian.

Sắp xếp và phân nhóm

Trong các tình huống cần sắp xếp người hoặc vật thành các nhóm có số lượng cố định, phép chia có dư cho biết số nhóm đầy đủ và số người/vật còn lại. Ví dụ, nếu có 50 học sinh cần chia thành các nhóm 8 người, ta có 6 nhóm đầy đủ và còn 2 học sinh (50 ÷ 8 = 6 remainder 2). Thông tin này giúp giáo viên hoặc người tổ chức sắp xếp hợp lý.

Bài tập và phương pháp luyện tập

Để thành thạo phép chia có dư, học sinh cần thực hành đều đặn với nhiều dạng bài tập khác nhau. Happymath đã tổng hợp một số phương pháp luyện tập hiệu quả mà các em có thể áp dụng.

Bài tập cơ bản

Học sinh nên bắt đầu với các bài tập đơn giản như chia các số có hai chữ số cho số có một chữ số. Ví dụ: 25 ÷ 4, 38 ÷ 7, 19 ÷ 3. Sau khi đã thành thạo, các em có thể tiến tới các bài tập phức tạp hơn với số bị chia có ba hoặc bốn chữ số. Việc luyện tập từ dễ đến khó giúp học sinh xây dựng sự tự tin và kỹ năng một cách vững chắc.

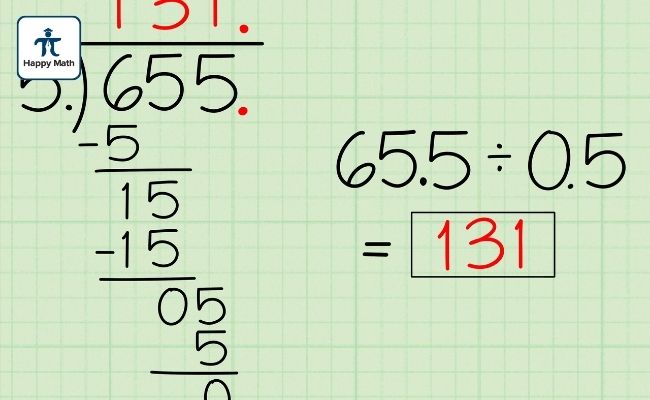
Học sinh cần thực hành đều đặn với nhiều dạng bài tập khác nhau

Bài tập ứng dụng

Bài tập ứng dụng (word problems) giúp học sinh kết nối kiến thức toán học với các tình huống thực tế. Ví dụ: "A bakery has 156 cookies and wants to pack them into boxes of 12. How many full boxes can they make and how many cookies will be left over?" Những bài toán như vậy không chỉ rèn luyện kỹ năng tính toán mà còn phát triển khả năng đọc hiểu và tư duy logic.

Kiểm tra kết quả

Một kỹ năng quan trọng là biết cách kiểm tra kết quả của phép chia có dư. Học sinh có thể sử dụng công thức dividend = (divisor × quotient) + remainder để xác minh đáp án. Ví dụ, nếu tính được 47 ÷ 6 = 7 remainder 5, ta kiểm tra: (6 × 7) + 5 = 42 + 5 = 47. Kết quả đúng với số bị chia ban đầu, chứng tỏ phép tính chính xác.

Sai lầm thường gặp khi học phép chia có dư

Trong quá trình học và thực hành phép chia có dư, học sinh thường mắc phải một số sai lầm phổ biến. Việc nhận biết và tránh những sai lầm này sẽ giúp các em tiến bộ nhanh hơn.

Nhầm lẫn giữa thương số và số dư

Nhiều học sinh, đặc biệt là những em mới bắt đầu làm quen với phép chia có dư, thường nhầm lẫn giữa thương số và số dư khi viết kết quả. Các em cần nhớ rằng thương số là số lần số chia "chứa" trong số bị chia, còn số dư là phần còn lại không đủ để chia thêm. Việc ghi chú rõ ràng và sử dụng đúng thuật ngữ tiếng Anh sẽ giúp tránh nhầm lẫn này.

Số dư lớn hơn hoặc bằng số chia

Một sai lầm nghiêm trọng là để số dư lớn hơn hoặc bằng số chia. Điều này cho thấy phép chia chưa hoàn thành và thương số cần được tăng thêm. Học sinh cần kiểm tra kỹ và đảm bảo số dư luôn nhỏ hơn số chia trong mọi trường hợp.

Quên kiểm tra lại kết quả

Nhiều em có thói quen làm xong bài tập mà không kiểm tra lại, dẫn đến bỏ sót những lỗi sai không đáng có. Việc dành vài giây để kiểm tra bằng cách nhân thương số với số chia rồi cộng số dư sẽ giúp phát hiện sai sót kịp thời và nâng cao độ chính xác.

Học phép chia có dư cùng Happymath

Với hơn 10 năm kinh nghiệm trong việc giảng dạy toán tiếng Anh, Happymath tự hào là người đồng hành tin cậy của hàng nghìn học sinh trên khắp thế giới. Chúng tôi hiểu rằng mỗi học sinh có tốc độ học tập và phong cách tiếp thu kiến thức khác nhau, do đó các khóa học của Happymath được thiết kế linh hoạt, phù hợp với từng đối tượng học viên.

Đội ngũ giáo viên tại Happymath, dưới sự dẫn dắt của thầy Nguyễn Anh Đức - người sáng lập và giảng viên chính, cam kết mang đến những bài giảng chất lượng cao với phương pháp giảng dạy tâm lý và hiệu quả. Chúng tôi không chỉ truyền đạt kiến thức mà còn giúp học sinh xây dựng tư duy toán học logic, phát triển khả năng giải quyết vấn đề và tự tin hơn khi học toán tiếng Anh.

Các bạn có thể truy cập happymath.edu.vn để khám phá thêm nhiều bài học, bài tập và tài liệu học tập phong phú về phép chia có dư cùng nhiều chủ đề toán học khác. Đừng quên theo dõi Happymath trên Youtube, Facebook, Instagram và Tiktok để cập nhật những kiến thức mới nhất và nhận được sự hỗ trợ tận tình từ đội ngũ giáo viên.

Phép chia có dú là một kiến thức nền tảng quan trọng trong toán học, và việc nắm vững nó sẽ mở ra cánh cửa cho nhiều kiến thức nâng cao hơn trong tương lai. Hãy để Happymath đồng hành cùng bạn trên con đường chinh phục môn toán tiếng Anh đầy thú vị này!