Phép tính với số thập phân - Decimal Operations

Số thập phân là một phần không thể thiếu trong toán học, xuất hiện từ những bài toán đơn giản trong cuộc sống hàng ngày đến các phép tính phức tạp trong khoa học và kỹ thuật. Việc thành thạo các phép tính với số thập phân không chỉ giúp học sinh nắm vững kiến thức toán học mà còn phát triển tư duy logic và khả năng giải quyết vấn đề. Bài viết này sẽ hướng dẫn chi tiết về các phép tính cơ bản với số thập phân, từ cộng trừ đến nhân chia, cùng những lưu ý quan trọng khi thực hiện các phép tính này.

Khái niệm về số thập phân (Decimal numbers)

Trước khi đi sâu vào các phép tính, việc hiểu rõ bản chất của số thập phân là vô cùng quan trọng. Số thập phân là cách biểu diễn các số không nguyên, giúp chúng ta mô tả chính xác các giá trị nằm giữa hai số nguyên liên tiếp.

Số thập phân là một phần không thể thiếu trong toán học

Cấu trúc của số thập phân

Một số thập phân bao gồm hai phần chính được ngăn cách bởi dấu chấm thập phân (decimal point). Phần bên trái dấu chấm gọi là phần nguyên (whole number part), còn phần bên phải là phần thập phân (decimal part). Ví dụ, trong số 15.67, số 15 là phần nguyên và 67 là phần thập phân. Mỗi chữ số sau dấu chấm thập phân đại diện cho một giá trị vị trí cụ thể: chữ số đầu tiên là hàng phần mười (tenths), chữ số thứ hai là hàng phần trăm (hundredths), và tiếp tục với hàng phần nghìn (thousandths).

Đọc và viết số thập phân

Kỹ năng đọc và viết số thập phân đúng cách là nền tảng để thực hiện các phép tính chính xác. Khi đọc số 3.25, chúng ta có thể đọc là "ba chấm hai năm" hoặc "ba và hai mươi lăm phần trăm". Trong tiếng Anh, số này được đọc là "three point two five" hoặc "three and twenty-five hundredths". Việc hiểu rõ cách đọc này giúp học sinh nắm bắt giá trị thực của số thập phân và tránh nhầm lẫn khi thực hiện các phép tính.

Mối quan hệ giữa số thập phân và phân số

Số thập phân có mối liên hệ chặt chẽ với phân số. Bất kỳ số thập phân nào cũng có thể được biểu diễn dưới dạng phân số và ngược lại. Ví dụ, 0.5 tương đương với 1/2, còn 0.75 tương đương với 3/4. Hiểu được mối quan hệ này giúp học sinh linh hoạt chuyển đổi giữa các dạng biểu diễn số, từ đó dễ dàng hơn trong việc giải quyết các bài toán thực tế.

Kỹ năng đọc và viết số thập phân đúng cách là nền tảng để thực hiện các phép tính

Phép cộng số thập phân (Addition of decimals)

Phép cộng là phép tính cơ bản nhất với số thập phân, và việc thực hiện chính xác phép cộng là bước đầu tiên để làm chủ các phép tính phức tạp hơn. Nguyên tắc quan trọng nhất khi cộng số thập phân là phải thẳng hàng dấu chấm thập phân.

Quy trình thực hiện phép cộng

Để cộng hai hoặc nhiều số thập phân, trước tiên cần viết các số sao cho các dấu chấm thập phân thẳng hàng theo chiều dọc. Điều này đảm bảo rằng các chữ số có cùng giá trị vị trí sẽ được cộng với nhau. Ví dụ, khi cộng 12.5 và 3.47, chúng ta viết 12.5 ở trên và 3.47 ở dưới, đảm bảo dấu chấm của cả hai số thẳng hàng. Nếu cần, có thể thêm số 0 vào cuối phần thập phân để cân bằng số chữ số, như viết 12.50 thay vì 12.5.

Thực hiện phép tính từ phải sang trái

Sau khi đã thẳng hàng các số, bắt đầu cộng từ hàng ngoài cùng bên phải, tương tự như cộng số nguyên. Cộng các chữ số ở mỗi hàng và nhớ sang hàng tiếp theo nếu tổng lớn hơn 9. Dấu chấm thập phân trong kết quả được đặt ngay dưới các dấu chấm thập phân của các số hạng. Ví dụ, 12.50 + 3.47 = 15.97, trong đó dấu chấm của kết quả nằm thẳng hàng với dấu chấm của các số hạng.

Các lỗi thường gặp

Nhiều học sinh mắc lỗi khi không thẳng hàng dấu chấm thập phân, dẫn đến việc cộng sai các chữ số. Một lỗi khác là quên đặt dấu chấm thập phân trong kết quả hoặc đặt sai vị trí. Để tránh những lỗi này, luôn kiểm tra lại việc thẳng hàng và đảm bảo dấu chấm trong kết quả nằm đúng vị trí.

Phép trừ số thập phân (Subtraction of decimals)

Phép trừ số thập phân tuân theo các nguyên tắc tương tự như phép cộng, với điểm khác biệt chính là thao tác lấy đi thay vì thêm vào. Việc thực hiện chính xác phép trừ đòi hỏi sự cẩn thận trong việc sắp xếp và tính toán.

Nguyên tắc thẳng hàng trong phép trừ

Giống như phép cộng, bước đầu tiên trong phép trừ là viết các số sao cho dấu chấm thập phân thẳng hàng theo chiều dọc. Số bị trừ (minuend) được viết ở trên và số trừ (subtrahend) ở dưới. Nếu hai số có số lượng chữ số thập phân khác nhau, thêm các số 0 vào cuối số có ít chữ số hơn để cân bằng. Ví dụ, khi tính 8.6 - 3.25, viết thành 8.60 - 3.25 để dễ dàng thực hiện phép tính.

Kỹ thuật mượn trong phép trừ

Khi chữ số ở hàng đang xét của số bị trừ nhỏ hơn chữ số tương ứng của số trừ, cần thực hiện phép mượn từ hàng bên trái. Quá trình mượn này giống hệt như trong phép trừ số nguyên, nhưng cần chú ý khi mượn qua dấu chấm thập phân. Ví dụ, trong phép tính 5.2 - 1.8, khi trừ 8 từ 2 ở hàng phần mười, cần mượn 1 từ hàng đơn vị, biến 5.2 thành 4.12, sau đó thực hiện 12 - 8 = 4.

Kiểm tra kết quả

Sau khi hoàn thành phép trừ, nên kiểm tra lại bằng cách cộng kết quả với số trừ để xem có bằng số bị trừ không. Phương pháp kiểm tra này giúp phát hiện và sửa chữa các sai sót trong quá trình tính toán.

Phép nhân số thập phân (Multiplication of decimals)

Phép nhân số thập phân có phần phức tạp hơn phép cộng và trừ vì cần xác định vị trí dấu chấm thập phân trong tích. Tuy nhiên, với phương pháp đúng, học sinh có thể dễ dàng thành thạo phép tính này.

Thực hiện phép nhân không cần thẳng hàng

Khác với phép cộng và trừ, khi nhân số thập phân, không cần thiết phải thẳng hàng dấu chấm thập phân. Thay vào đó, thực hiện phép nhân như với số nguyên, tạm thời bỏ qua dấu chấm. Ví dụ, khi nhân 2.5 với 3.4, có thể nhân 25 với 34 để được 850.

Xác định vị trí dấu chấm trong tích

Sau khi có tích của các số nguyên, đếm tổng số chữ số sau dấu chấm thập phân của cả hai thừa số. Dấu chấm trong tích sẽ được đặt sao cho số chữ số sau dấu chấm bằng tổng này. Trong ví dụ trên, 2.5 có 1 chữ số thập phân và 3.4 cũng có 1 chữ số thập phân, tổng là 2. Do đó, đặt dấu chấm vào 850 để có 2 chữ số thập phân, kết quả là 8.50 hay 8.5.

Nhân với lũy thừa của 10

Một trường hợp đặc biệt quan trọng là nhân số thập phân với 10, 100, 1000 hoặc các lũy thừa khác của 10. Khi nhân với 10^n, chỉ cần dịch chuyển dấu chấm thập phân sang phải n vị trí. Ví dụ, 3.45 × 10 = 34.5, còn 3.45 × 100 = 345. Quy tắc này giúp tính toán nhanh chóng mà không cần thực hiện phép nhân truyền thống.

Phép chia số thập phân (Division of decimals)

Phép chia là phép tính phức tạp nhất trong các phép tính với số thập phân, đòi hỏi sự hiểu biết sâu sắc về cấu trúc số và kỹ năng tính toán chính xác. Có hai trường hợp chính: chia một số thập phân cho một số nguyên và chia giữa hai số thập phân.

Chia số thập phân cho số nguyên

Khi chia một số thập phân cho một số nguyên, thực hiện phép chia như bình thường, nhưng phải đặt dấu chấm thập phân trong thương ngay phía trên dấu chấm của số bị chia. Ví dụ, khi chia 12.6 cho 3, đặt dấu chấm trong thương thẳng hàng với dấu chấm của 12.6, sau đó thực hiện phép chia để được kết quả 4.2.

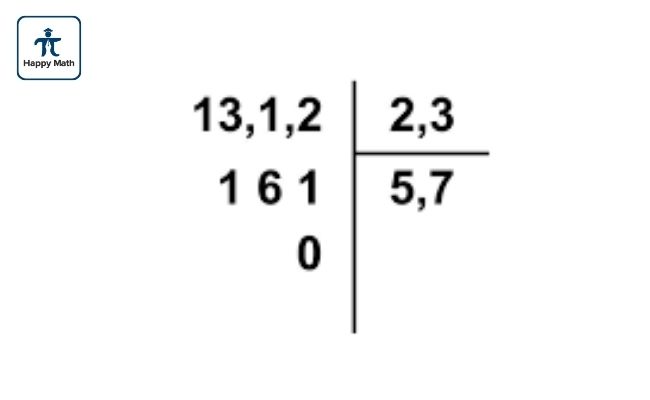
Phép chia là phép tính phức tạp nhất trong các phép tính với số thập phân

Chia cho số thập phân

Khi số chia là một số thập phân, cần chuyển đổi nó thành số nguyên trước khi thực hiện phép chia. Nhân cả số bị chia và số chia với cùng một lũy thừa của 10 để số chia trở thành số nguyên. Ví dụ, để chia 8.4 cho 0.7, nhân cả hai số với 10 để được 84 chia cho 7, kết quả là 12. Phương pháp này đơn giản hóa phép chia mà không làm thay đổi giá trị của thương.

Phép chia không hết và làm tròn

Nhiều phép chia số thập phân không cho kết quả hết, dẫn đến thương có vô số chữ số thập phân. Trong những trường hợp này, cần làm tròn kết quả đến một số chữ số thập phân nhất định theo yêu cầu. Quy tắc làm tròn cơ bản là: nếu chữ số tiếp theo lớn hơn hoặc bằng 5, làm tròn lên; nếu nhỏ hơn 5, giữ nguyên.

Ứng dụng thực tế của phép tính số thập phân

Các phép tính với số thập phân không chỉ là lý thuyết trên giấy mà xuất hiện thường xuyên trong cuộc sống hàng ngày. Từ việc tính tiền mua sắm, đo lường kích thước, đến các tính toán trong khoa học và kỹ thuật, số thập phân đóng vai trò quan trọng.

Ứng dụng trong tài chính

Trong các giao dịch tài chính, số thập phân được sử dụng để biểu diễn số tiền với độ chính xác đến từng xu. Khi mua sắm, tính tổng hóa đơn, hoặc tính lãi suất ngân hàng, đều cần thực hiện các phép tính với số thập phân. Ví dụ, nếu một sản phẩm giá 15.75 đô la và bạn mua 3 sản phẩm, tổng số tiền là 15.75 × 3 = 47.25 đô la.

Ứng dụng trong đo lường

Các phép đo trong thực tế thường cho kết quả là số thập phân. Khi đo chiều dài, khối lượng, thể tích hoặc nhiệt độ, cần sử dụng số thập phân để đạt độ chính xác cần thiết. Trong xây dựng, kiến trúc, và kỹ thuật, việc tính toán chính xác với số thập phân là yếu tố quan trọng đảm bảo chất lượng công trình.

Các phép đo trong thực tế thường cho kết quả là số thập phân

Ứng dụng trong khoa học

Các tính toán khoa học thường đòi hỏi độ chính xác cao với nhiều chữ số thập phân. Từ việc tính toán khối lượng phân tử trong hóa học, vận tốc trong vật lý, đến xác suất trong thống kê, số thập phân là công cụ không thể thiếu. Hiểu rõ và thành thạo các phép tính với số thập phân giúp học sinh chuẩn bị tốt cho các nghiên cứu khoa học trong tương lai.

Kết luận

Phép tính với số thập phân là kỹ năng toán học cơ bản nhưng vô cùng quan trọng, ảnh hưởng đến nhiều khía cạnh trong cuộc sống và học tập. Việc nắm vững các phép cộng, trừ, nhân, chia với số thập phân không chỉ giúp học sinh đạt kết quả tốt trong các kỳ thi mà còn trang bị cho các em những công cụ thiết yếu để giải quyết các vấn đề thực tế. Thông qua việc thực hành thường xuyên và áp dụng vào các tình huống cụ thể, học sinh sẽ dần phát triển sự tự tin và thành thạo trong việc làm việc với số thập phân.

Tại Happymath.edu.vn, chúng tôi cam kết đồng hành cùng học sinh trong hành trình chinh phục toán học tiếng Anh. Với đội ngũ giảng viên giàu kinh nghiệm và phương pháp giảng dạy tâm lý, chúng tôi mong muốn giúp mỗi học sinh không chỉ hiểu rõ các phép tính với số thập phân mà còn yêu thích bộ môn toán học. Hãy truy cập website của chúng tôi để khám phá thêm nhiều bài học bổ ích và tài liệu học tập chất lượng về toán tiếng Anh.